What is Tributary Area?

The Tributary area is the area around the column that is surrounded by the centerline, which transfers the load of the column to the ground.

Let us consider the slab supported by the beam and column as an example. The amount of load transferred to any member can be determined using the tributary area (loading) concept. The shape of the supporting area is determined by the geometry of the formation.

Most often, designers use the tributary area to calculate the load transfer from the slab to the column and to calculate the reactions of the framing beams of the column.

Columns and beams play a major role in buildings because their purpose is to safely transfer different types of loads from the structure to the ground below. When the load falls to the ground, they are transferred to the solid surface of the earth by the foundations.

Different types of loads are applied to the column, such as structure load (dead load), floor and beam weight, furniture and equipment, wind, snow, and earthquake (environmental load), etc.

Part of the floor is carried by various columns. How much load each column carries? For the calculation of all these things, the tributary area method is used.

Also Read: Catslide Roof | What Is Catslide Roof? | Advantages & Disadvantages of Catslide Roof

Tributary Area in Column:

The center plan of the column is given as shown in the figure in which the area around the column shown from the centerline of the panel is shown with different properties.

which is the supporting area of the column, which is given to transfer the load through the column in the middle of the area. The Tributary Area of a Column is dead supported load is equal to the dead load per unit area of the auxiliary field.

How to Calculate Tributary Areas:

Calculating the exact tributary area, first, we have to understand how the forces flow through the slab. Just like a wider river has more capacity to transport water, a stiffer column has more carry capacity to “transport” (or transfer) more forces. Additionally, the slab can also have different stiffnesses in different directions by beam, making the flow non-uniform.

This method From each given point of the slab, find the point closest to the column.

This method Finds the point closest to the column from each given point of the slab. This is done by drawing a midline and dividing the distance in half by the column. The area on the side with the centerline column will be its ‘Tributary area.’

The midpoint between each pair of these pairs is found. And a perpendicular line is drawn based on it. Thus perpendicular lines are drawn in front of each column. The tributary area should be defined in this way.

Also Read: What Is Roof Valley? | Roof Valley Installation | Types of Roof Valleys | Repairing Roof Valleys

The Tributary Area Can Be Determined by Following the Simple Steps Below

Identify the neighboring columns in each direction attached to each column in the given drawing.
Measure the distance between the pairs of these two columns.
Divide the distance between the pairs of these two columns by 2.
Draw a line perpendicular to the center in this way.
Now repeat each pair of columns for gridlines like this.

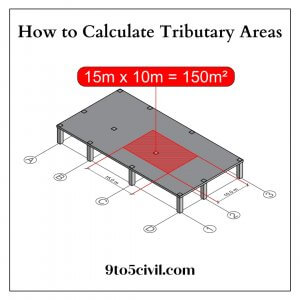
Tributary Area Example:

Let us understand with an example how to calculate the tributary load of auxiliary areas. See this article. Please observe the figure below.

The shape of a slab is usually rectangular, and when the columns are arranged parallel to the edge of the slab. The centerline is directed from the grid in the plan. The constructive grid is made up of 4 grid lines in one direction and 3 grid lines in the other direction. Each grid line has a column at the intersection.

Also Read: What Is a Sawtooth Roof? | How to Build a Sawtooth Roof? | Advantages & Disadvantages of Sawtooth Roofs

Let us calculate Colum D-1 as a tributary area,

First of all, the neighbors of the column in each direction are identified.
The neighboring columns c1 and d2 of the D-1 column are located.
Now the distance between D-1 and C-1 is given as 16 meters, and the distance between D-1 and D-2 is given as 8 meters.
Now, this column D-1 and C-1 will get half distance 16/2 = 8 meters, and a half distance between D-1 and D-2 will be 8/2 = 4 meters.
When drawing perpendicular lines with the help of midpoints.

Following the steps above, we end up with two lines marked in red that appear in the figure.

As you can see in the figure below, two drawn lines intersect at one point. This point defines an angle of the auxiliary field because column D-1 is located at an angle.

The other corners of the rectangle are defined by the outer boundary of the slab.

The boundary hatch is a rectangle, so we calculate the side length by multiplying.

Column D-1 = 8m x 4m = tributary area of 32 M²is obtained.

Thus tributary load calculator the repeating this process for columns can be found for all columns.

Conclusion

In this article, we have adopted a simple geometric approach for calculating column auxiliary areas. This method is approximate, and the auxiliary column is assumed to be equally rigid. This slab is supposed to carry loads evenly in all directions. The structure of the example shown in the article also simplifies regular calculations.

Like this post? Share it with your friends!

Suggested Read –

Frequently Asked Questions (FAQ)

What Is Tributary Load?

Tributary load calculation or tributary width represents the accumulation of loads. Which is directed towards a specific structural member of any building.

Tributary Area Calculation

Follow the Easy Steps Below to Determine the Tributary Area:

Calculate the separation between the pairs of these two columns.
The separation between these two columns’ pair distances should be divided by 2.
In this technique, draw a line parallel to the center.
Repeat each set of columns to create gridlines.

What Is Tributary Area Formula?

Tributary area is the area that a structural element supports and that contributes to the applied loads on that element12. The tributary area formula depends on the type of element and the load distribution. For a roof with a uniform pressure load, the tributary area given roof live load is calculated by At = 1000* (1.2- (Lf/ (20*R2))), where Lf is the roof live load, R2 is the reduction factor for slope of roof, and 1000 is a conversion factor34.

How to Find the Tributary Area of a Column?

To solve this problem, we can identify every column’s neighbor, and divide the distance in half by drawing a centerline. The area on the columns side of the centerline will be its’ tributary area.

What Is the Tributary Area of a Beam?

Tributary width definition: Tributary loading or tributary width refers to the accumulation of loads on a particular structural member. Example: If the tributary width is 6 feet + 8 feet = 14 feet and the load is 100 PSF then the load on the beam will be 14 feet x 100 PSF = 1400 PLF.

How to Find Tributary Area?

The tributary area is equal to the unit length of the tributary width. The load w that supports the length of that unit is equal to the pressure load q times the tributary area (1 * t w).

What Is Tributary Area of Roof?

The tributary area of roof plays an important role in planning the floor or ceiling. Which shows the loading on a specific structural element.

What Is Tributary Area?